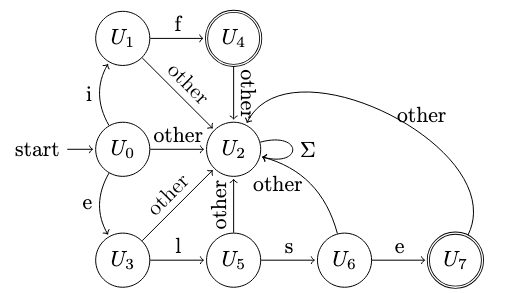
Compiler-As-1
Question 1
Let
| Current State | ||
|---|---|---|
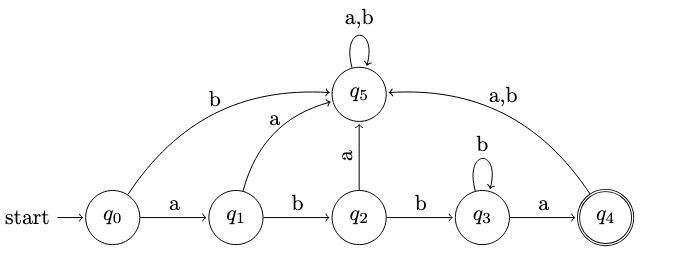
| Current State | ||
|---|---|---|
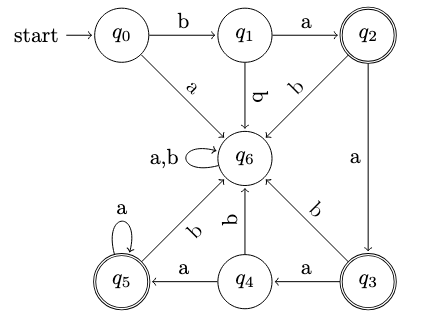
| Current State | ||
|---|---|---|
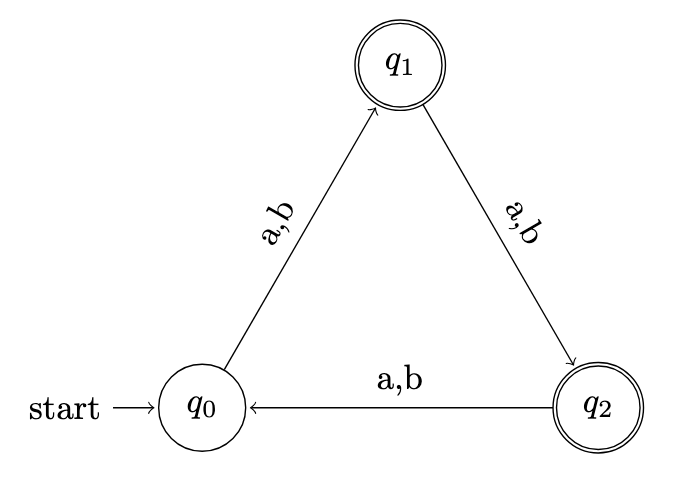
Question 2
Design a regular expression for each language in Q1. (6 marks for each)
a.
Question 3
Let
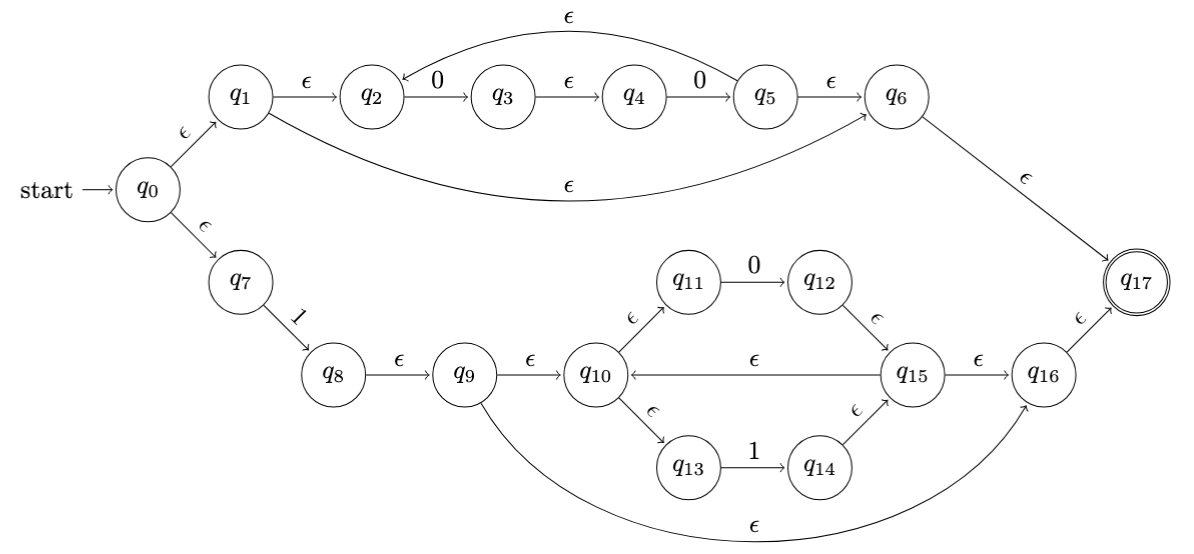
Question 4
Given the following NFA
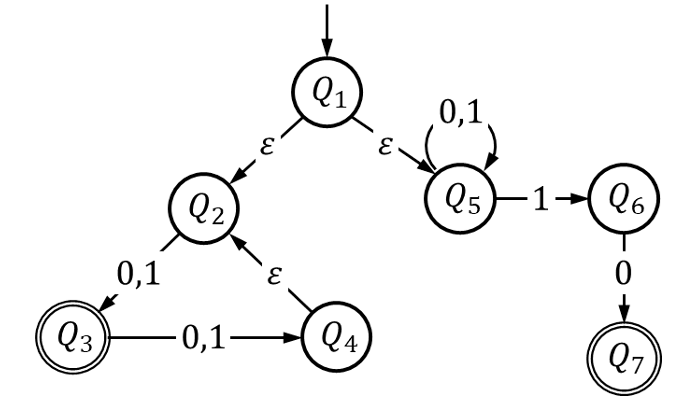
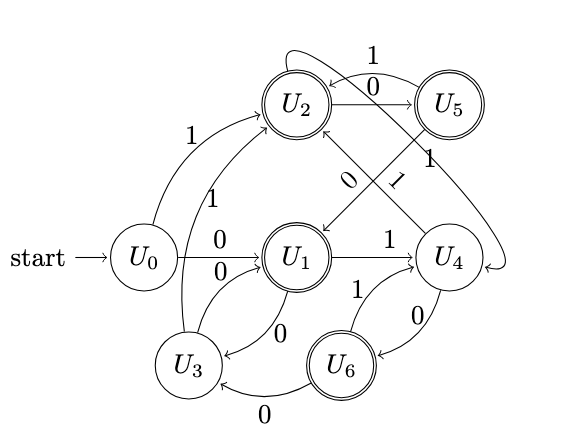
a. Convert the NFA to the equivalent DFA. (20 marks)
First iteration
Second iteration
Third iteration
Fourth iteration
Fifth iteration
Sixth iteration
Seventh iteration
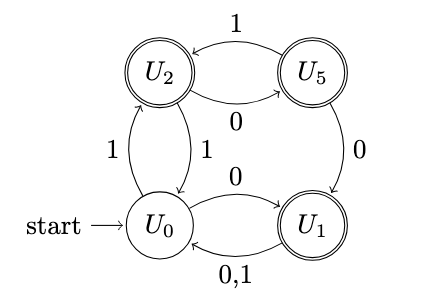
b. Minimize the DFA in part a). (20 marks)
Initially,
Finally, the minimized DFA is:
Question 5
Consider a new alphabet
a. Design a DFA with a trap state which recognizes the keywords if or else. (The DFA does not accept any other string.) (10 marks)